はじめに

この記事では， Signed Distance Field の計算をします。
内容は薄めなのです。

方眼紙を押し込む

私たちの目に見えている世界は，輪郭も色も滑らかです。 その中に存在しているはずのピクセル画像は，その縁をなぞると，でこぼこしています。

拡大するとギザギザしていますし，グラデーションをよく見ると継ぎ目が見えてしまいます。 様々な大きさの画面が存在する世界でこの縁に触れてしまうと，じんわりと痛みが走ります。

今回は，この輪郭を綺麗にすることを考えてみます。

Signed Distance Field（以下SDF）という「場」があります。

これは符号付きの無次元量であり，物体の表面からの距離に比例します。 この場を高さ0で切り取った等高線は，その物体の輪郭となります。 当然，任意の次元に対して計算できるものですが，今回は2次元の画像について考えてみます。 3次元のボクセルは可視化が難しいですからね。

SDFで表現することで，ピクセル画像は真に斜めの線を表現できます。
その代わりに失われている物がある事にも気を付けてくださいね。

そう，色です。

計算する

ひとまず実装したものがこれです。

基本的には以下の工程を，内外を裏返して2回行っています。

各ピクセルは，一番近い内部ピクセル座標（以下「最短座標」）と，
そこまでの距離（以下「最短距離」）を持ちます。

1. 内側の全てのピクセルに対し，
	1.1. 「最短距離は0」「最短座標は自分自身」と記録します。
	1.2. 座標をキューに詰めます。
2. 幅優先探索で，キューから座標を取り出します。
	2.1. 上下左右のピクセルに対し，最短座標を教えます
	2.2. 自分が知っている最短座標の方が相手から見て近い場合，
		2.2.1. 最短座標と最短距離を更新します。
		2.2.2. 最短距離が更新されたピクセルをキューに詰めます。

つまりは，方眼紙の交点をノードと見なしたグラフで dijkstra 法を行っています。

今回はC++23で実装しましたけれど，もし実装する際にはお好みの言語を使ってみてください。

引っ張る

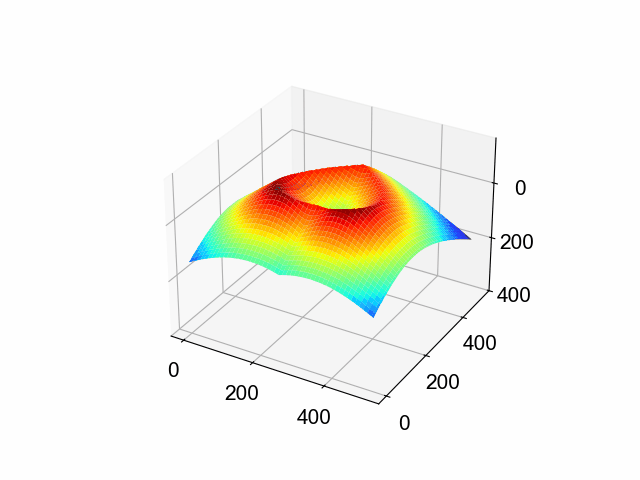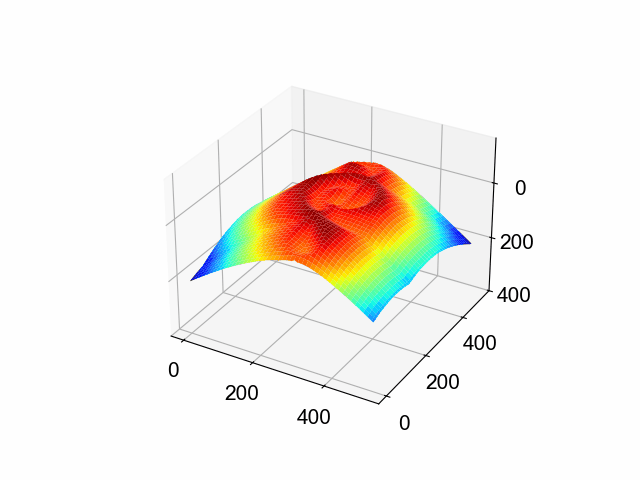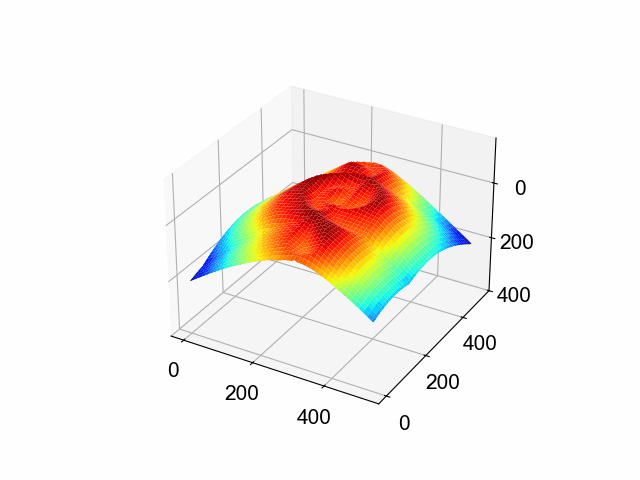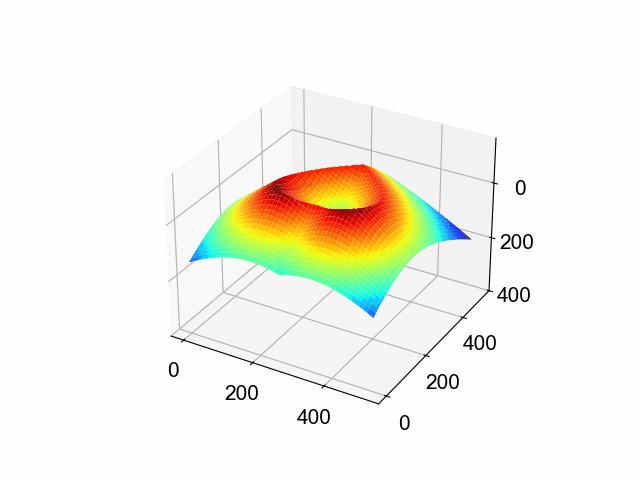
例えば，「★」のSDFは，このような形をしています。

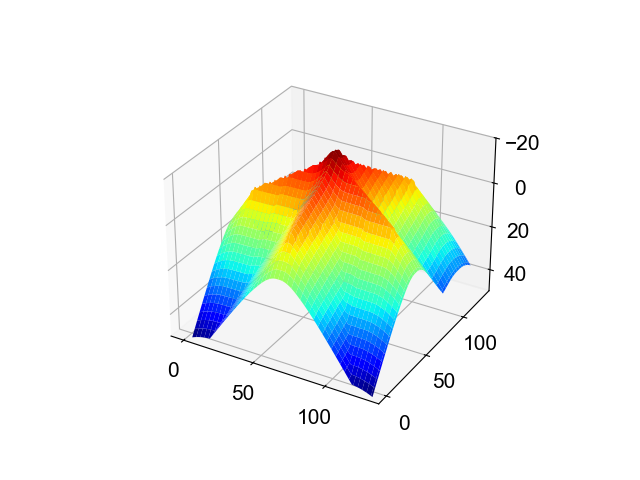
同様に，「↑」のSDFは，このような形をしています。

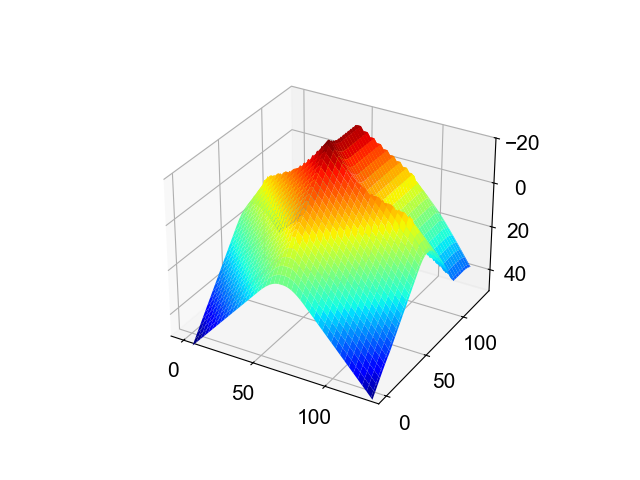
普段画像を重ね合わせる際，色の中間状態を取っているはずです。

では，これらの中間状態を取るとどうなるのでしょうか。

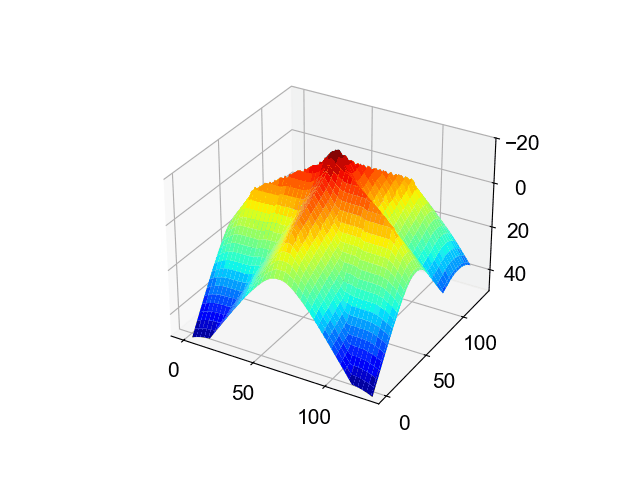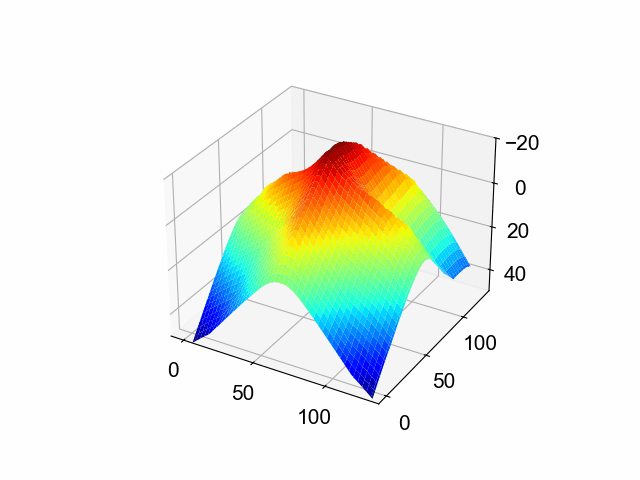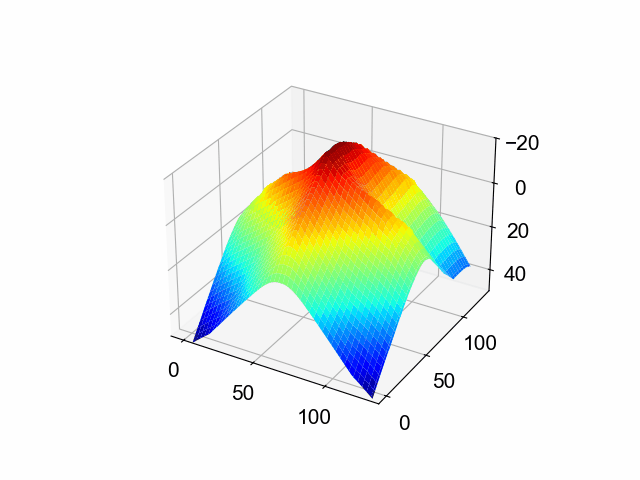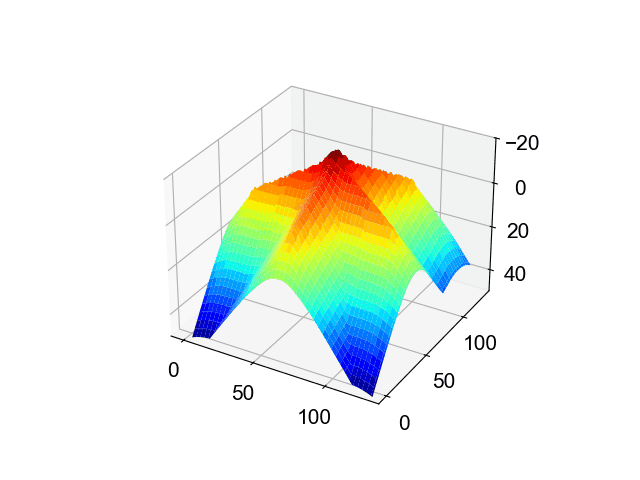
答えは明快で，断面の形は滑らかに切り替わります。
滑らかといっても，鋭角の移り変わりかたに多少の痛みを感じます。 これは線形補間によるものです。

この滑らかさは，トポロジーの維持とは全く関係ありません。 例えば，全く無関係な形同士でモーフィングさせてみると，このように滲んだような表現になります。

何か面白い応用例が浮かんだら教えて頂けると，そっと喜びます。

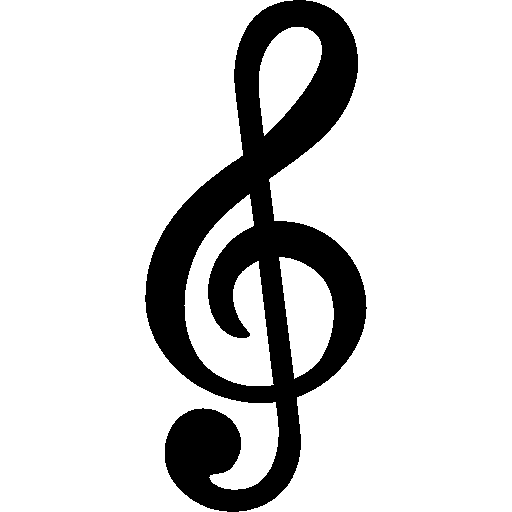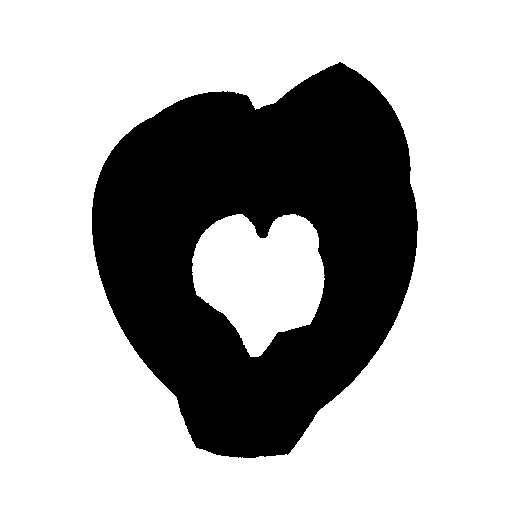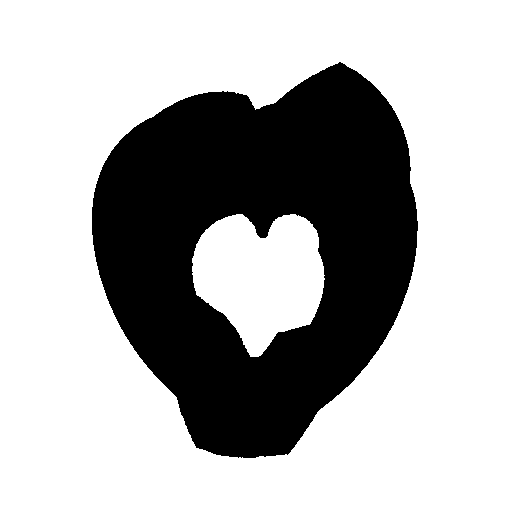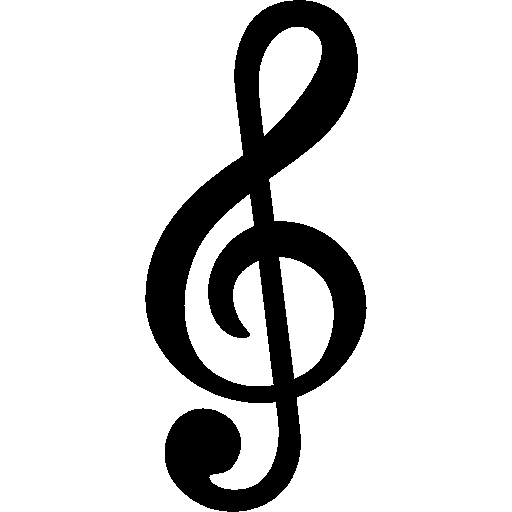
今回は，「色を犠牲にして形を表現する」記事を書こうと思ったのですが，題材が単純であったため，実質的に幅優先探索の実装練習のようになってしまいました。
この手法は一般の次元で適用できますので，ボクセルのモーフィングなども，そのうち試してみますね。

それでは。